Batch 2 - Class 320 - Slippery Snail, Silver Dollar and NIM Games
zoom: send meeting Id and password
Start recording
Preclass Exercise:
(In class)
Attendance: Anika, Yatharth, Vansh, Kabir, Aarushi, Adyant, Vivaan, Ekagra, Savya, Aneesh, Tarush, Ayush, Rhea, Ryan, Aarav, Advay, Nikhil
Class Notes:
Recap slippery snail
- With 4 bugs in slippery snail, we saw those as two sets, and like two piles of stones from which we are taking away a few. As long as we could keep the distances between bugs in each set the same, we can win
- What if there are 6 bugs?
Silver Dollar
- Let kids play a few games
- What is the winning strategy
- Do you see parallels between this and the slippery snail game?
- Talk about equivalence of problems, and its applications, for example in NP hard problems like traveling salesman, graph coloring and halting problem (https://en.wikipedia.org/wiki/NP-completeness)
- What if there were 6 steps to the ladder?
Stone piles
- Play the game where there are two piles of stones, and a player can remove any number of stones from one pile. The player who finishes the stones first wins
- Do you see the parallel between the slippery snail and silver dollar games?
- What if there were 3 piles of stones?
- In 2 piles, making the piles equal represents something in binary math. What is it?
- Can we extend that to 3 piles? If required play the game with students couple of times, and ask them to write the binary representations of numbers in each pile. See if they observe a pattern to your moves
- The trick is to make the binary sum 0000. Same thing that we were doing in two piles
- Now can we extend this solution to slippery snail and silver dollar?
- What are the differences between the stones and slippery snail problem that are important to consider? Establishing equivalence has to be a thorough exercise!
Homework:
- (536Dudeney - 319) The fly at point A below take a minute to crawl an edge of the cube. How long will it take it to reach point B?
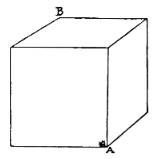
- Answer: 2.236 minutes along the diagonal
References: